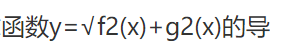请输入或粘贴题目内容
搜题
拍照、语音搜题，请扫码下载APP
题目内容
（请给出正确答案）
设f和g都是群(G1，★)到群(G2，*)的同态映射，证明：(C，★)是(G1，★)的一个子群，其中，C={x|x∈G1，且f(x)=g(x)}．
答案
任取x，y∈C，则有f(x)=g(x)以及f(y)=g(y)，而
f(x★y-1)=f(x)*f(y-1)=f(x)*f(y)-1=g(x)*g(y)-1
=g(x)*g(y-1)=g(x★y-1)，
即x★y-1∈C，表明(C，★)是(G1，★)的子群．
更多“设f和g都是群（G1，★)到群（G2，*)的同态映射，证明：（C，★)是（G1，★)的一个子群，其中，C={x|x∈G1，且f（x)=g（x)}．”相关的问题
第1题
设f为从群(G1，*)到群(G2，△)的同态映射，证明：f为单射，当且仅当Ker(f)={e}．其中e是G1中的单位元．
第5题
设G与G'都是群，f是群G到G'的同态映射,a∈G.
(1)证明若a的阶是有限的,则f(a)的阶也是有限的，且|f(a)|、整除|a|.
(2)如果f(a)的阶是有限的，那么a的阶一定是有限的吗？证明你的结论.
第7题
设(H，*)和(K，*)都是群(G，*)的子群，证明(H∩K，*)也是(G，*)的子群。
第9题
已知G1(x，y，z)，G2(x，y，z)，f(x，y)都是可微的，
gi(x，y)=Gi(x，y，f(x，y))，i=1，2．
第10题
设(G，*)是一个群，H
且H中的元素都是有限阶的，运算在H中封闭，则(H，*)是(G，*)的子群．
